Les Jeux de Stratégie - Le Pathfinding
Le pathfinding consistera à trouver un chemin (pas nécessairement le meilleur) pour se rendre d'un point de la map à un autre automatiquement. Nous allons voir une approche simple et efficace, suffisante pour un jeu à base de tile.
1) Algorithme A-Star (A*)
En une phrase: c'est LA méthode la plus classique utilisée dans différents cas de figure. Il fonctionne très bien dans un graphe (en l'occurrence notre map à base de tile, quadrillée), et permet de se déplacer d'un point à un autre en proposant un chemin souvent proche de la perfection (selon la complexité du graphe). Le but sera de prendre le chemin qui se dirige le plus vers notre destination. Évidemment, il n'est pas exclut que l'algo devra rebrousser chemin si il arrive à une situation pas intéressante, mais dans la majorité des cas, c'est une très bonne méthode. De plus, il faut savoir ce que l'on cherche: le chemin le plus court, ou un temps de calcul raisonnable. Tester tous les cas permettrait à coup sur de trouver le meilleur chemin, mais à quel prix ? Il faut donc se baser sur des heuristiques (approximation), afin d'économiser du précieux temps de calcul (il n'y a pas que du pathfinding dans un jeu de stratégie !)
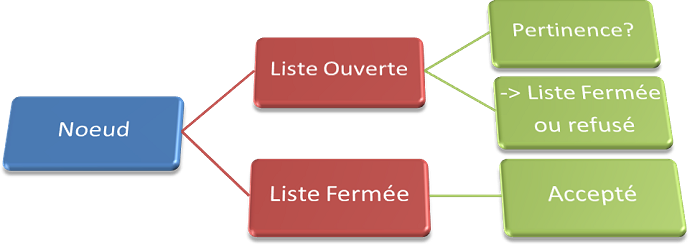
La recherche se base sur deux listes:
- Liste ouverte, contenant la liste des noeuds du graphe à étudier (sans doublon)
- Liste fermée, contenant la liste des noeuds faisant parti du meilleur chemin (après avoir été dans la liste ouverte uniquement)
Pour déterminer la pertinence d'un noeud, un bon choix consiste à regarder la distance entre le noeud à l'étude, et le dernier noeud validé, ainsi qu'avec la destination.
Il faut ensuite effectuer la somme de ces deux distances.
Plus cette somme est faible, plus le noeud est pertinent.
pertinence = dist(cur_node, last_valid_node) + dist(cur_node, destination)
Pour chaque noeud, on étudie tous ses voisins dans la liste ouverte, et on place le meilleur (meilleur pertinence) dans la liste fermée. Si un voisin est bloquant (obstacle) ou est déjà dans la liste fermée, on l'ignore. Ce dernier servira de nouveau point de départ pour l'étape suivante, et ainsi de suite. Si lors de la construction de la liste fermée on s'éloigne de la destination, il faudra alors 'rebrousser' chemin, et recommencer en faisant un autre choix.
Si la destination est atteinte, alors l'algorithme peut s'arrêter. Sinon, il continue jusqu'à ce qu'aucune solution ne soit bonne (aucun chemin trouvé).
2) La Map en tant que Graphe
Nous avons vu que l'algorithme A* s'appliquait très bien dans un graphe. Mais qu'en est-il de notre map à base de tile ? Les tiles sont des carrés, la map n'est finalement qu'un graphe de sous graphes complets (chaque noeud possède le même nombre de sommets adjacents, 8 avec les diagonales)
Exemple de recherche de chemin du point D au point F:

Lire la suite: Les Jeux de Stratégie - La Production